Diagram Venn Komplemen Himpunan

Komplemen dari himpunan a yaitu 0 1 6 7. Diagram venn merupakan cara untuk menyatakan himpunan dengan gambar diagram. Teori himpunan yang baru diciptakan pada akhir abad ke 19 sekarang merupakan bagian yang tersebar dalam pendidikan matematika yang mulai diperkenalkan bahkan sejak tingkat sekolah dasar.

plant animal prokaryotic cell venn diagram powerpoint venn diagram overlap color printable venn diagram 3 circles printable lined venn diagram plant and animal cell venn diagram worksheet problem sums on venn diagram problem solving venn diagrams 3 circles pengertian dari diagram venn

Mengenal Diagram Venn Rumushitung Com

Himpunan Dan Diagram Venn Idschool

Pengertian Dan Contoh Soal Himpunan Komplemen Berpendidikan Com

Assalamu Alaikum Wr Wb Ppt Download

14 Perhatikan Diagram Venn Berikuthimpunan Komplemen Dari Aub Adalah A 1 2 3 4 5 6 7 B Brainly Co Id

Berdasarkan Diagram Venn Tersebut Tentukan Banyak Anggota Daria A Komplemenb B Komplomenc C Brainly Co Id

Dengan pembentuk notasi himpunan dapat dituliskan a x x î s x ï a.

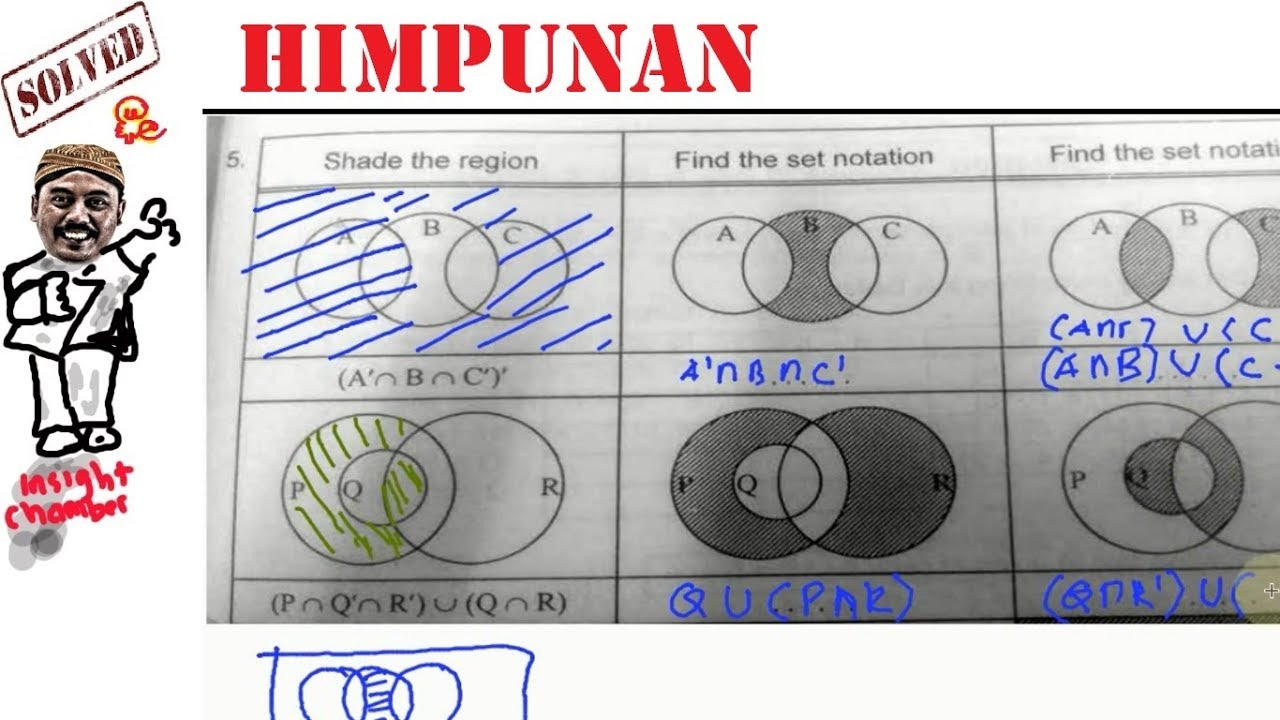
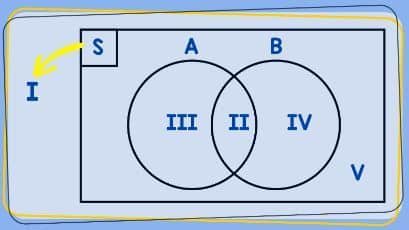
Diagram venn komplemen himpunan. Dalam diagram venn ada empat hubungan antara himpunan termasuk gabungan irisan komplemen himpunan dan selisih dalam himpunan. Irisan seperti misalnya himpunan a 0 1 2 3 4 5 dan himpunan b 3 4 5 6 7. Dalam sebuah diagram venn ada sekitar 4 hubungan antar himpunan yaitu irisan gabungan komplemen himpunan dan juga selisih himpunan. Himpunan semesta digambarkan dengan segiempat dan himpunan.

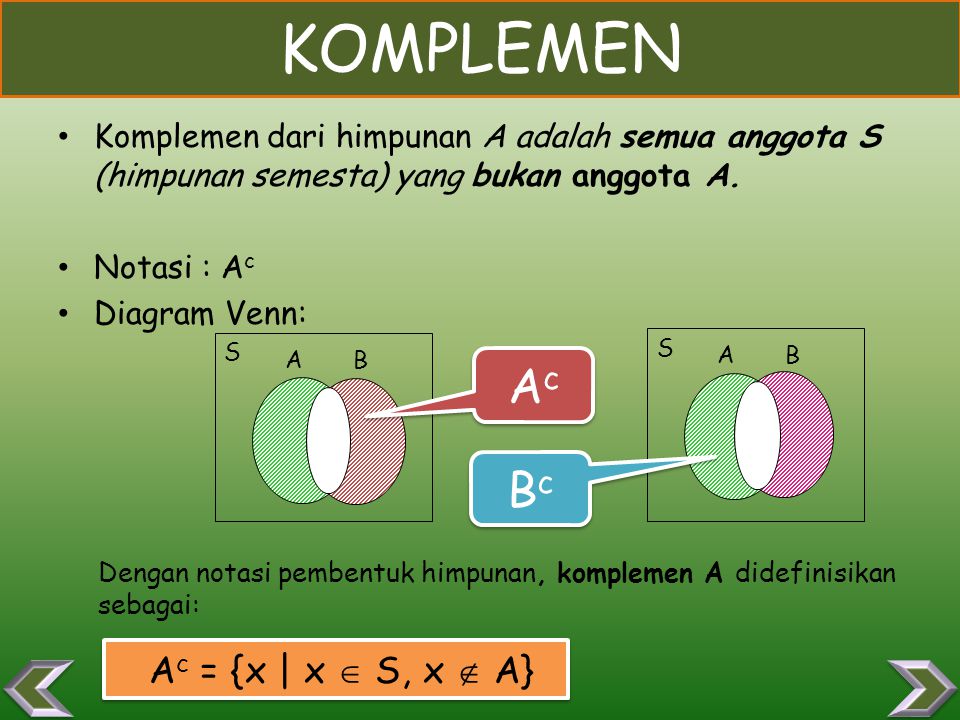
A c x x u dan x a atau. Setiap anggota himpunan dinyatakan dengan noktah titik nama anggota ditulis di dekat noktah. Komplemen himpunan a adalah suatu himpunan yang anggotaanggotanya merupakan anggota s tetapi bukan anggota a. Diagram venn penyajian himpunan dengan diagram venn ditemukan oleh seorang ahli matematika inggris bernama john venn tahun 1881.

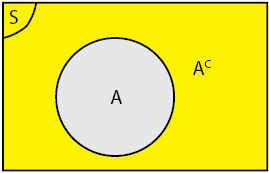
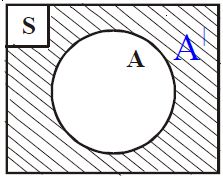
Jika kita nyatakan dalam diagram venn yaitu sebagai berikut. Himpunan 1 2 6 7 juga merupakan komplemen jadi ac 1 2 6 7. Perhatikan diagram venn di bawah ini daerah yang diarsir adalah komplemen dari a atau a. Jika anggota himpunan banyak noktah noktahnya tidak perlu digambar.

Komponen dari himpunan a tersebut dinotasikan atau ditulis dengan a yang dibaca a komplemen atau komplemen dari a. Pembahasan lengkap tentang materi rumus himpunan pengertian himpunan diagram venn jenis himpunan irisan himpunan operasi himpunan dan cara menyatakan. Komplemen suatu himpunan agar anda dapat memahami mengenai komplemen suatu himpunan coba ingat kembali pengertian himpunan semesta atau semesta pembicaraan. Misalkan u 1 2 3 4 9 jika a 1 2 4 maka a c 3 5 6 7 8 9.

Komplemen dari a terhadap s ditulis a baca komplemen dari a atau a komplemen. Teori himpunan dapat dianggap sebagai dasar yang membangun hampir semua aspek dari matematika dan merupakan sumber dari mana semua matematika. Komplemen a juga bisa dinyatakan dengan diagram venn. Teori ini merupakan bahasa untuk menjelaskan matematika modern.

Misalnya a adalah himpunan yang berada pada semesta pembicaraan u maka komplemen dari himpunan a dinotasikan sebagai berikut. Dengan notasi pembentuk himpunan dituliskan sebagai berikut. Pada diagram venn berlaku aturan berikut. Himpunan komplemen jika di misalkan s 1 2 3 4 5 6 7 dan a 3 4 5 maka a.

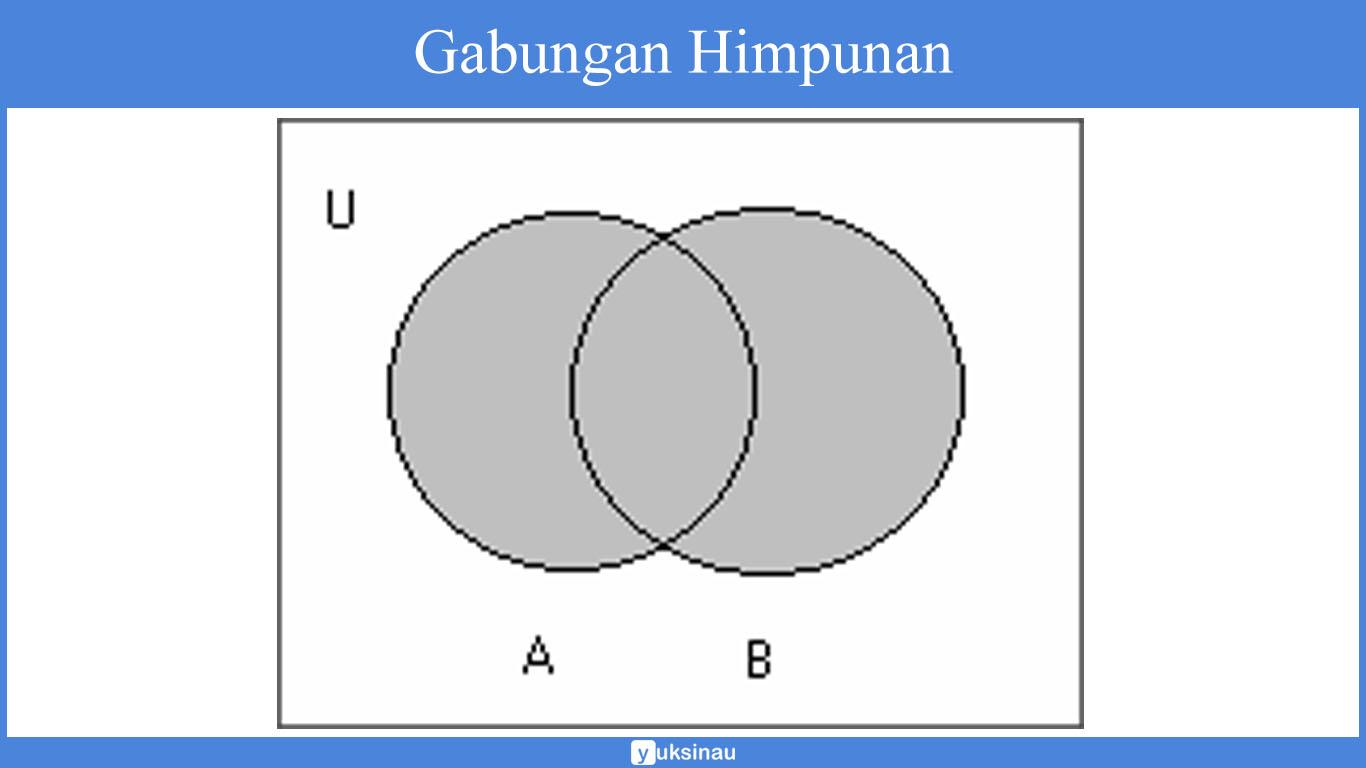
Gabungan himpunan a dan b ditulis dengan a b adalah jumlah yang anggotanya ditetapkan ke a atau anggota himpunan b atau keduanya. Yang dapat dilihat pada gambar berikut.