Number Diagram Complex

This is a real number but this tells us how much the i is scaled up in the complex number z right over there.

Number diagram complex. The real numbers are complex numbers with an imaginary part of zero. This video will explain how to tackle questions on complex numbers specifically the argand. In mathematics the complex plane or z plane is a geometric representation of the complex numbers established by the real axis and the perpendicular imaginary axis. The set of complex numbers includes all the other sets of numbers.

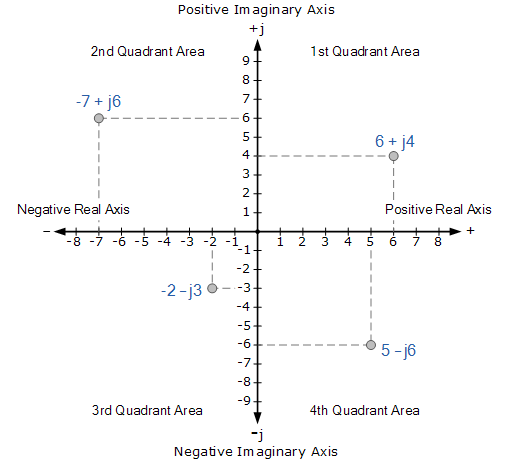
Analogous to the cartesian plane is the argand diagram also called the complex plane where the horizontal axis is the real part of a number and the vertical axis is the imaginary part. R x 2 y 2 θ tan 1 y x to convert from polar to cartesian form. The following diagram shows how complex numbers can be plotted on an argand diagram. Complex numbers such as 2 3i have the form z x iy where x and y are real numbers.

Then a complex number consists of two distinct but very much related parts a real number plus an imaginary number. Re is the real axis im is the imaginary axis and i satisfies i 2 1. It was devised by the swiss mathematician jean robert argand about 1806. The horizontal axis is called the real axis while the vertical axis is called the imaginary axis.

Under addition they add like vectors. X is called the real part and y is called the imaginary part. The complex plane is a plane with. What is an argand diagram.

An argand diagram is a plot of complex numbers as points. It can be thought of as a modified cartesian plane with the real part of a complex number represented by a displacement along the x axis and the imaginary part by a displacement along the y axis. Complex numbers represent points in a two dimensional complex or s plane that are referenced to two distinct axes. Argand diagram graphic portrayal of complex numbers those of the form x yi in which x and y are real numbers and i is the square root of 1.

Now one way to visualize complex numbers and this is actually a very helpful way of visualizing it when we start thinking about the roots of numbers especially the complex roots is using something called an argand diagram. Imaginary numbers running up down. The concept of the complex plane allows a geometric interpretation of complex numbers. This video will explain how to tackle questions on complex numbers specifically the argand diagram.

A similar representation had been proposed by the danish surveyor caspar wessel. The complex number z x yi is plotted as the point x y where the real part is plotted in the horizontal axis and the imaginary part is plotted in the vertical axis. X r cos θ y r sin θ polar form r cos θ i r sin θ is often shortened to r cis θ.