Properties Of Intersection Of Sets With Examples

In theorem 5 30 we will prove some properties of set operations for indexed families of sets.

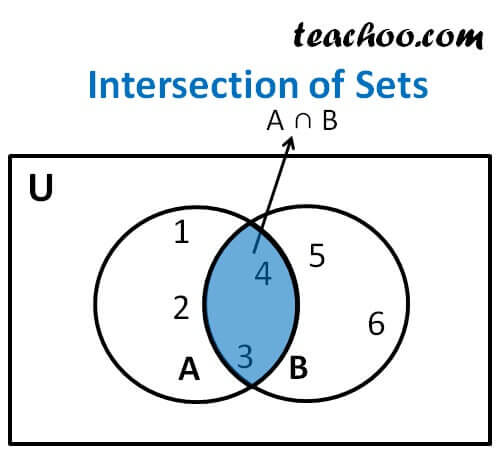
Properties of intersection of sets with examples. To make it easy notice that what they have in common is in bold. The following table gives some properties of union of sets. For example a mathematician might be interested in knowing about sets s and t without caring at all whether the two sets are made of baseballs books letters or numbers. Intersection of sets a b has all the elements which are common to set a and set bit is represented by symbol let a 1 2 3 4 b 3 4 5 6 a b 3 4 the blue region is a bproperties of intersectiona b b a commutative law a b c a b c associative law a.

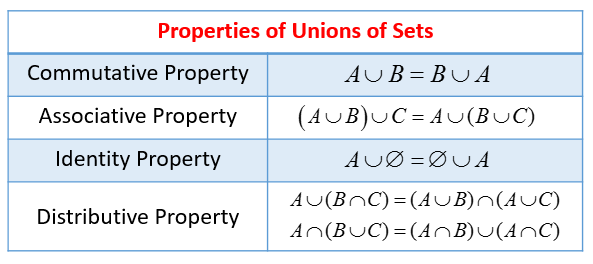
Scroll down the page for examples and solutions. Properties of union and intersection. Some of these properties are direct extensions of corresponding properties for two sets. Given two sets a and b the intersection is the set that contains elements or objects that belong to a and to b at the same time.

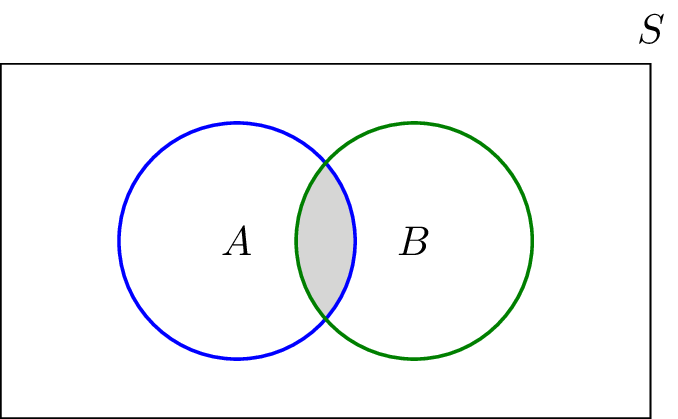
But certainly expertise to solve the problem special tools techniques and tricks as well as knowledge of all the basic concepts are required to obtain a solution following are some of the operations that are performed on the sets. The intersection property of the empty set says that any set intersected with the empty set gives the empty set. The intersection of two sets a and b denoted by a b is the set of all elements that is common to both a and b. In mathematical form for two sets a and b a b x.

X is a natural number less than 0. Next we illustrate with examples. For example we have already proved de morgan s laws for two sets in theorem 5 20. Forming the symmetric difference of two sets is simple but forming the symmetric difference of three sets is a bit trickier.

X a and x b similarly for three sets a b and c. The following venn diagrams show the complement of the intersection of two sets and the complement of the intersection of three sets. Basically we find a b by looking for all the elements a and b have in common. The algebra of sets defines the properties and laws of sets the set theoretic operations of union intersection and complementation and the relations of set equality and set inclusion it also provides systematic procedures for evaluating expressions and performing calculations involving these operations and relations.

Any set of sets closed under the set theoretic operations forms a. The union of two sets a and b is the set of elements which are in a or in b or in both. We write a b. It is denoted by a b and is read a union b.

Set theory is the field of mathematics that deals with the properties of sets that are independent of the things that make up the set. Let a 3 7 11 and b x. A a.