Verify De Morgan S Law By Venn Diagram

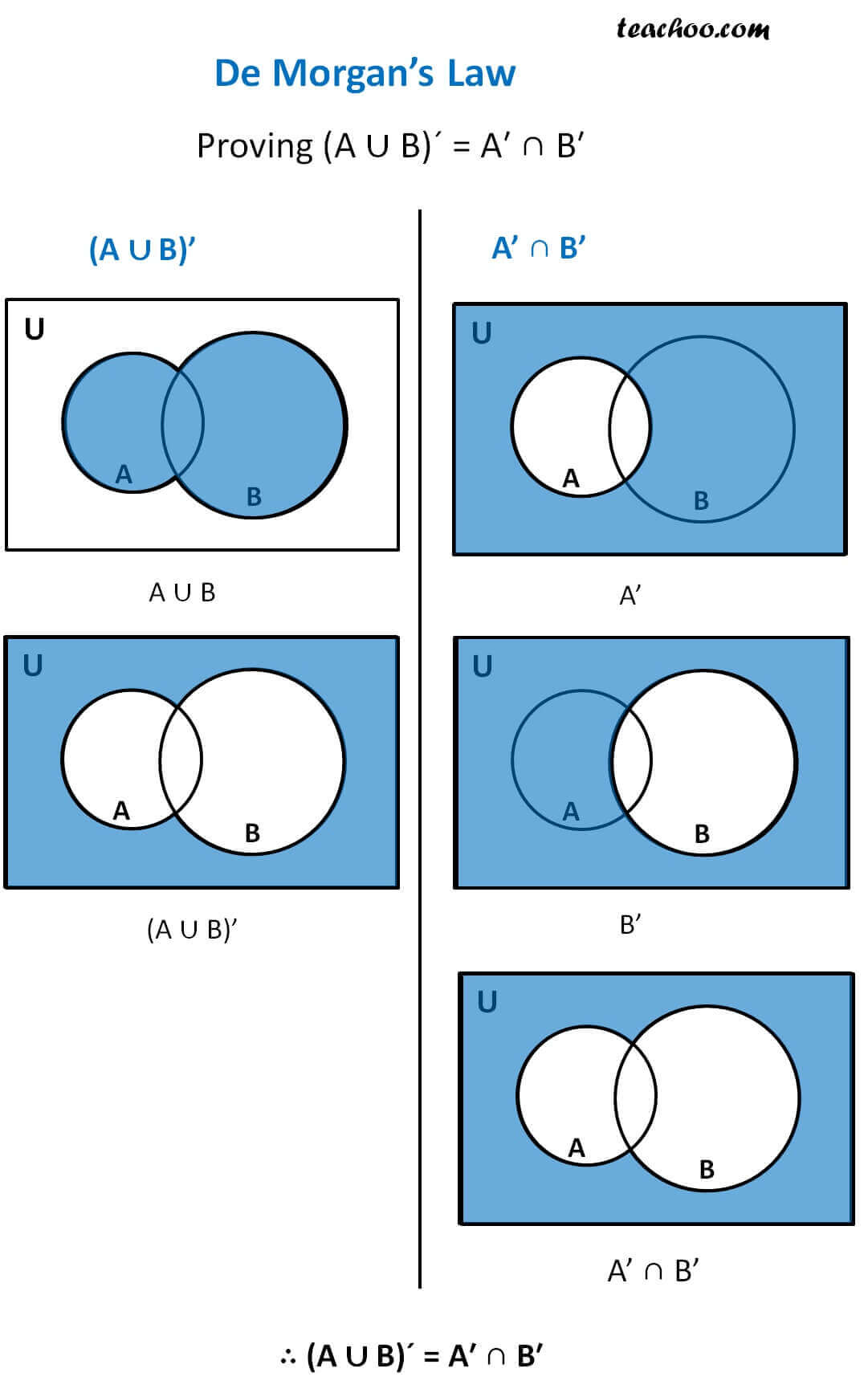
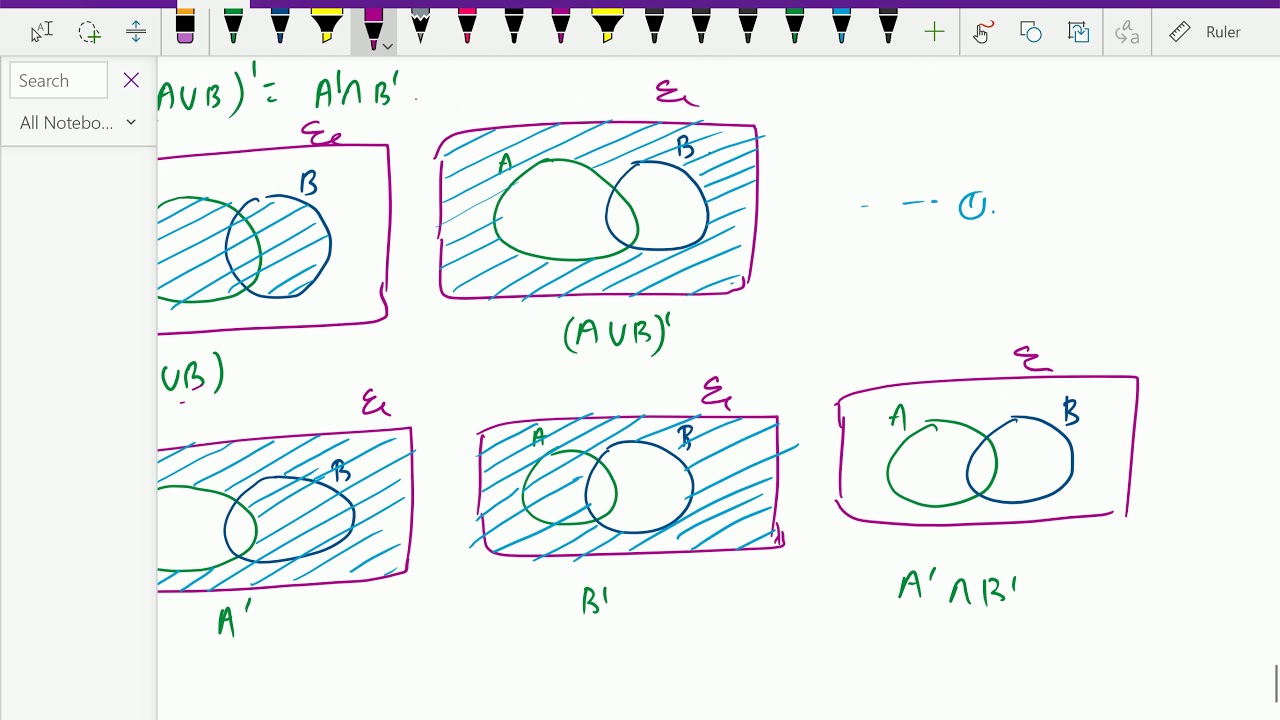
He says that the compliment of a or b is equivalent to the covenant of a intersected with coming to be.

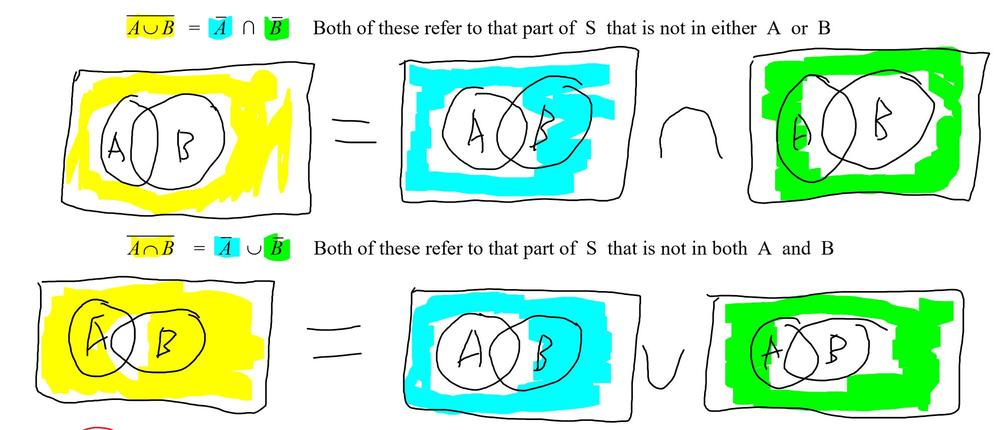
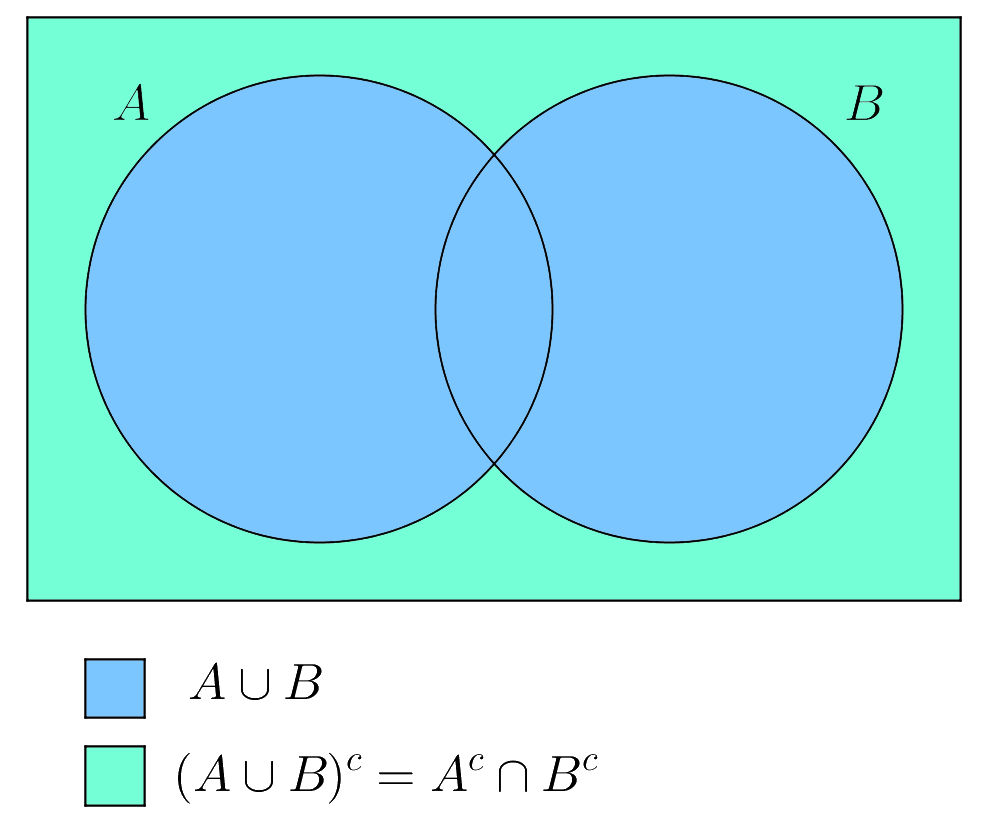
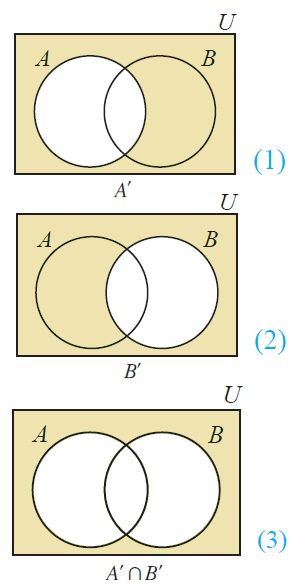
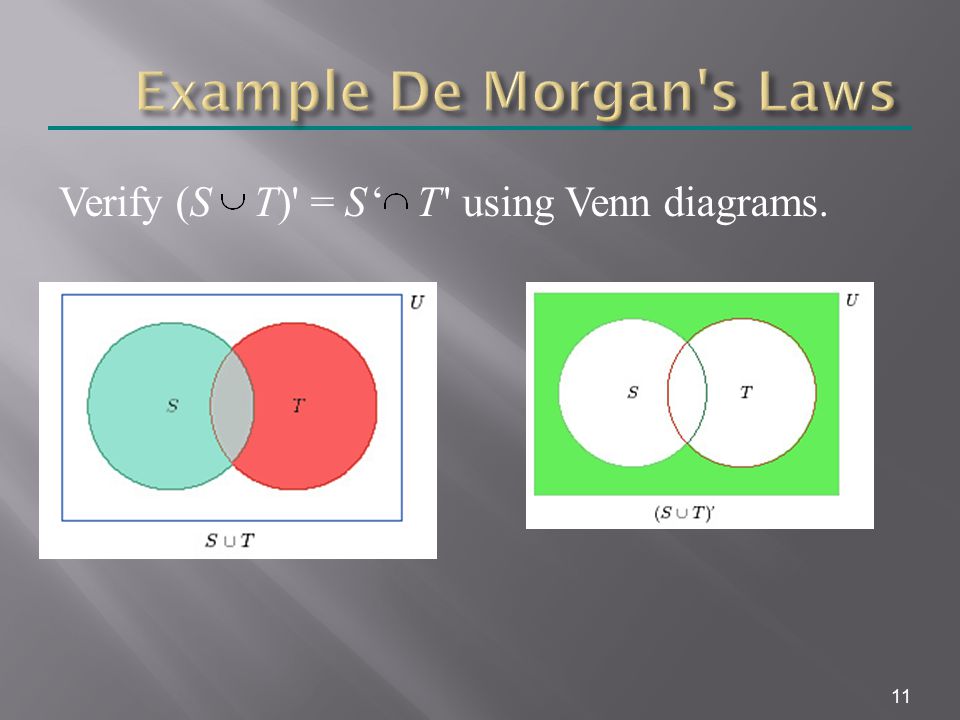
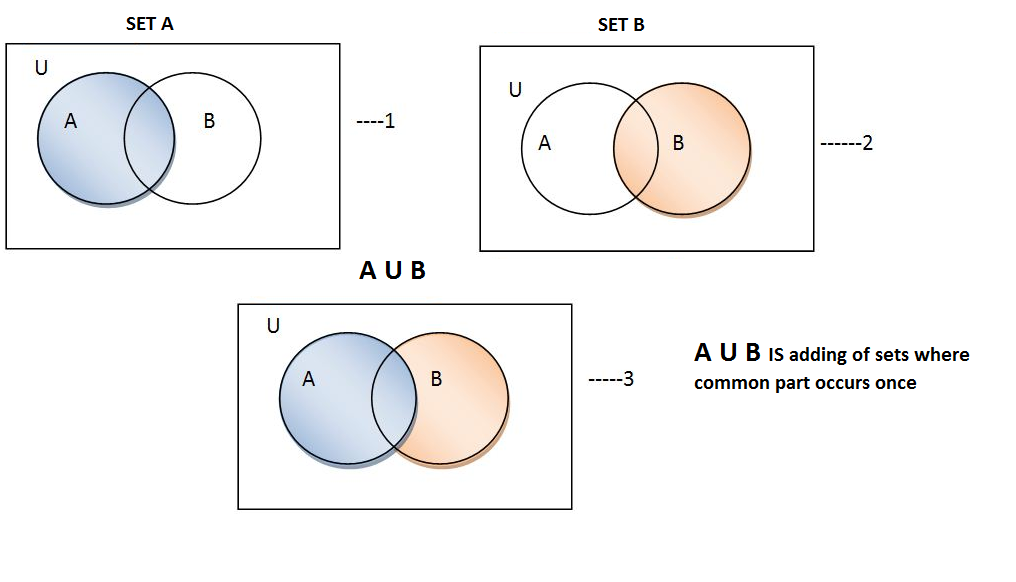
Verify de morgan s law by venn diagram. De morgan s laws in set theory states that complement of the union of two sets is equal to the intersection of co. Let s draw this out in venn diagrams to really get a sense of what this represents first listed on the sample space and now we ll draw two sets a. Let s validate to morgan s laws using venn diagrams. From the above venn diagrams 2 and 5 it is clear that a n b a u b hence de morgan s law for complementation is verified.

Augustus de morgan 1806 1871 was born in madurai tamilnadu india. De morgan s father a british national was in the service of east india company india. Click here to get an answer to your question use venn diagrams to verify de morgan s law of complementation a b a b 11th. First let s state to morgan s first law.

Now to the second part of the law which is the same as. Great explanation on de morgans law. In propositional logic de morgan s laws relate conjunctions and disjunctions of propositions through negation. Learn the explanation to de morgan s laws.

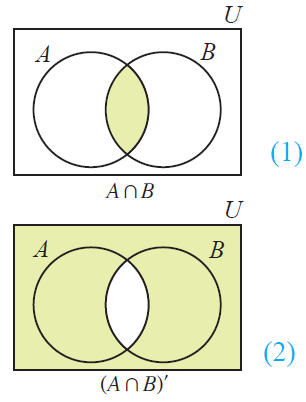
Let us take the first part of this equation and represent it in a venn diagram. Applied to set theory de morgan s law states let s dig deeper into this law. In set theory de morgan s laws relate the intersection and union of sets through complements. About de morgans law for set difference de morgans law for set difference.

Here we are going to see de morgan s law for set difference. The venn diagram example graphics helps a lot to understand this the standard way. The rules can be expressed in english as. Using venn diagrams to verify set identities including de morgan s law the probability identity of either of two events happens or both happen by definition the sample space contains all possible outcomes of an experiment.

Venn diagrams to verify. Consider set a and set b. De morgan s laws describe how mathematical statements and concepts are related through their opposites. De morgan s laws are also applicable in computer engineering for developing logic gates.

In propositional logic and boolean algebra de morgan s laws are a pair of transformation rules that are both valid rules of inference they are named after augustus de morgan a 19th century british mathematician the rules allow the expression of conjunctions and disjunctions purely in terms of each other via negation. April 16 2015 at 12 48 am.