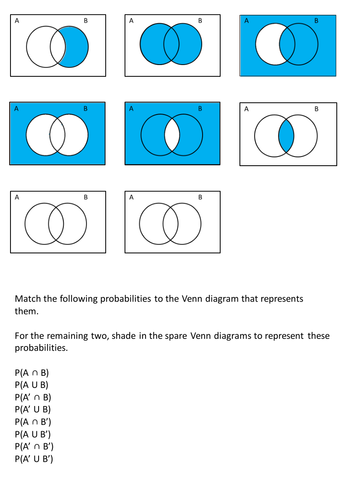
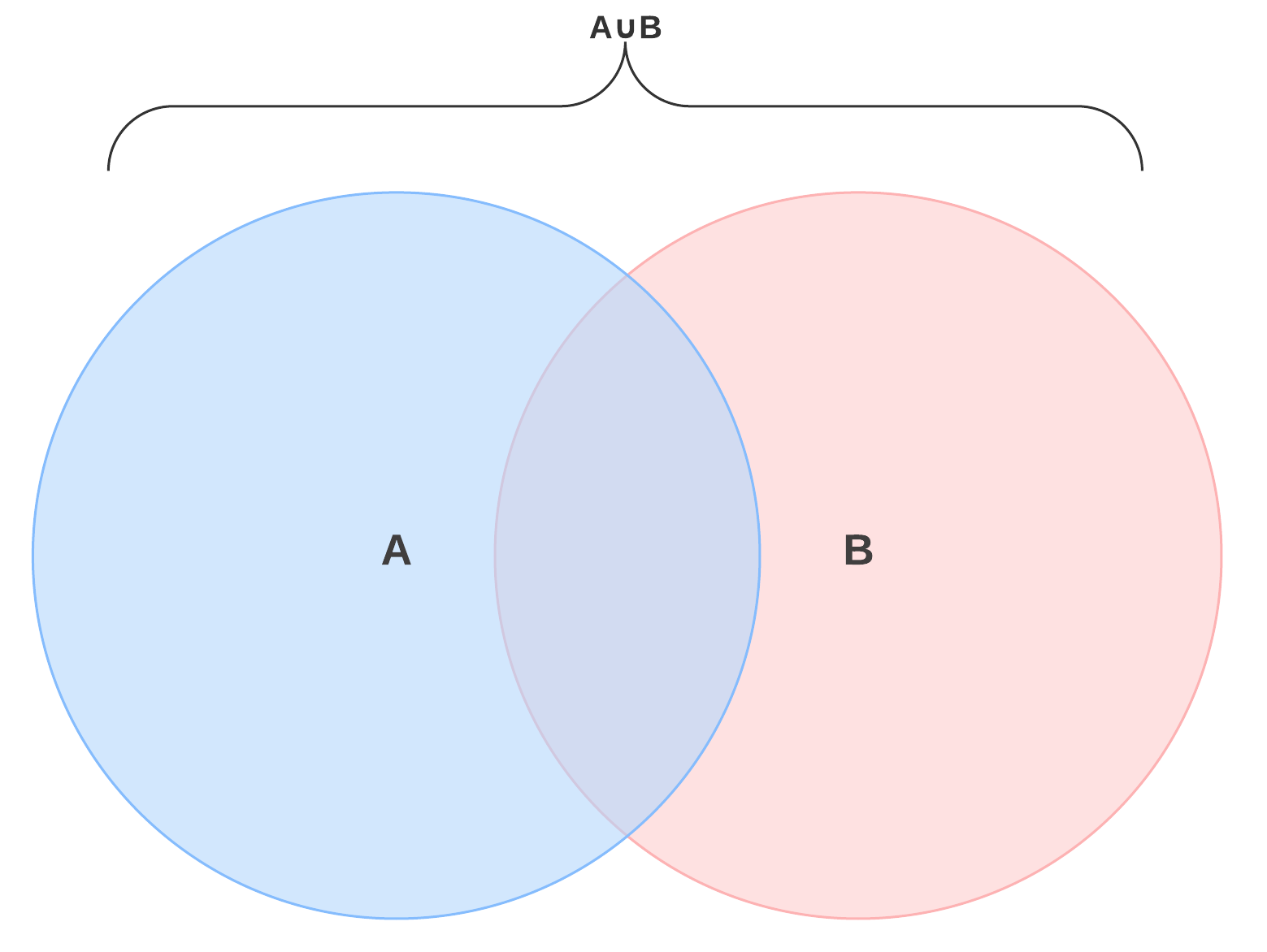
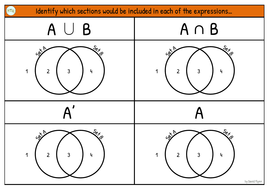
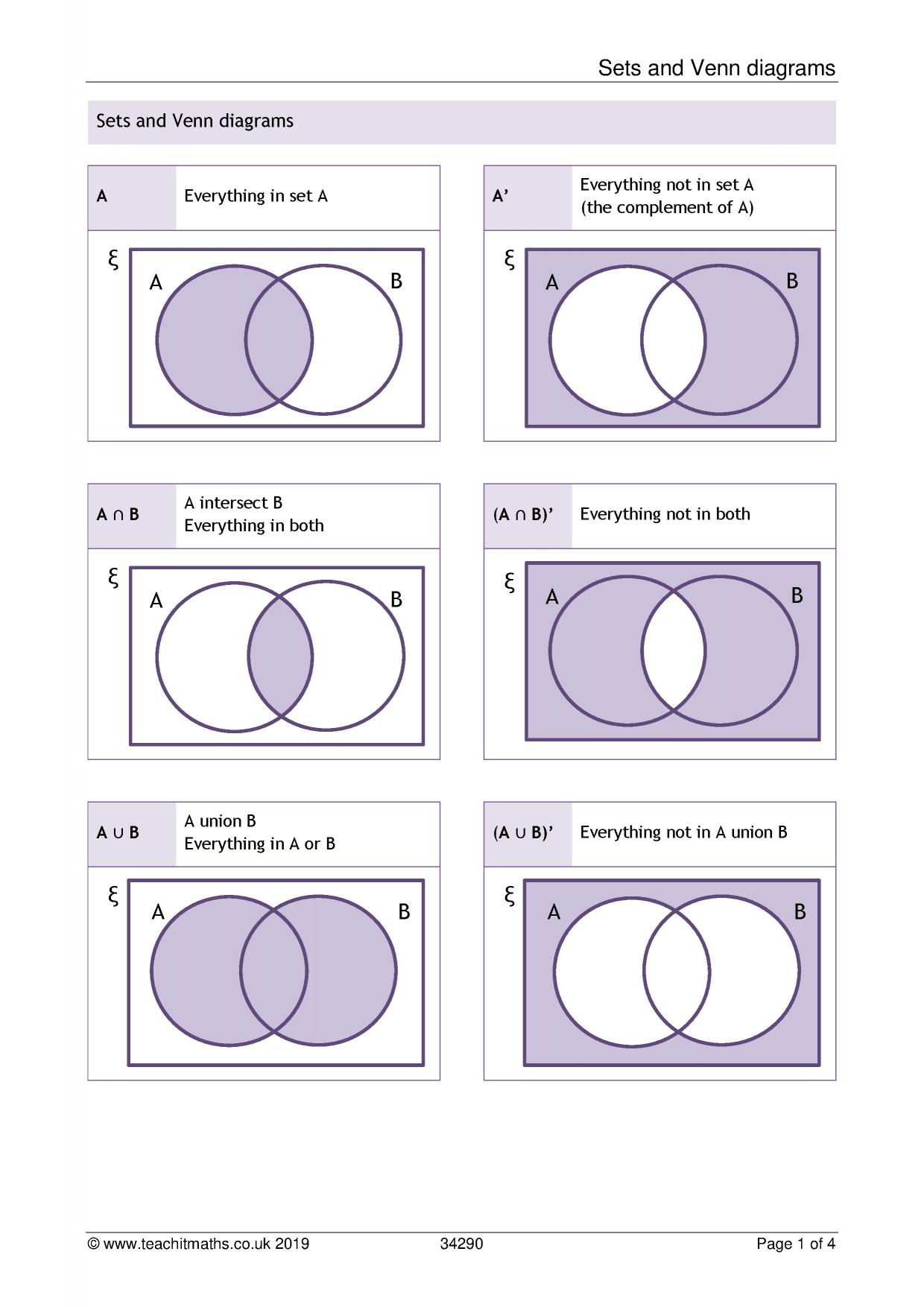
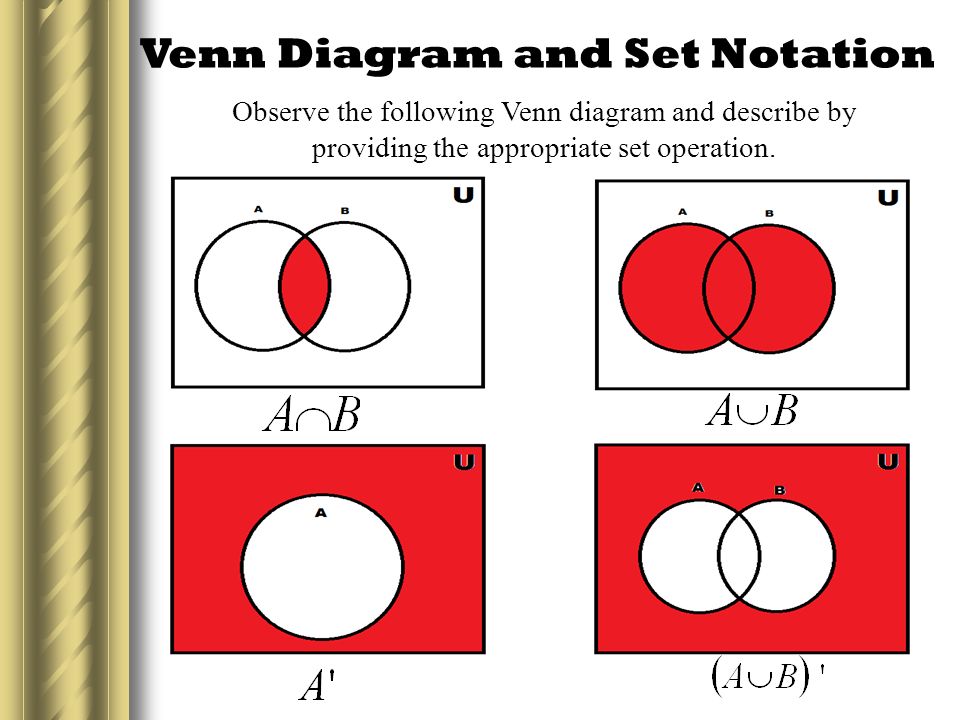
Venn Diagram Notation Meaning

Use set notation to describe. For sets a b and c the union is written as a b c. A venn diagram also called primary diagram set diagram or logic diagram is a diagram that shows all possible logical relations between a finite collection of different sets these diagrams depict elements as points in the plane and sets as regions inside closed curves.

plant and animal cell venn diagram answers problems involving sets ppt purpose venn diagram template prove de morgan s law venn diagram prokaryotes vs eukaryotes venn diagram worksheet powerpoint editable venn diagram template parts of a cell venn diagram problem solving using venn diagram math

Clip 127 Venn Diagrams Notation Youtube

Venn Diagrams Corbettmaths Youtube

Gcse Tutorial Set Notation And Venn Diagrams Shading Intersections Higher And Foundation Youtube

Venn Diagrams New Gcse Teaching Resources

Unit 1 Section 4 Set Notation

Venn Diagram

A the area shaded in green b the area shaded in red.

Venn diagram notation meaning. For example the items you wear is a set. Look at the venn diagrams on the left. Sets and venn diagrams sets. The following examples should help you understand the notation terminology and concepts relating venn diagrams and set notation.

Venn diagrams can be used to express the logical in the mathematical sense relationships between various sets. B is the set of colors of the french flag. While there are more than 30 symbols used in set theory you don t need to memorize them all to get started. In fact the following three are the perfect foundation.

Once you have got to grips with these you will be able to arrange all sorts of groups and sets. Look at the venn diagrams on the left. A set is a collection of things. A the area shaded in blue b the area shaded in purple.

A is the set whose members are the first four positive integers. Using the basics we ll cover here you too can begin using venn diagrams in more complex ways. There are more than 30 symbols used in set theory but only three you need to know to understand the basics. Set builder notation is an example of intensional definition.

You write sets inside curly brackets like this. Look at the venn diagram on the left. You can also have the union for more than two sets. Venn diagrams represent mathematical sets.

On a venn diagram the union is every element within both circles. The union symbol venn diagrams are comprised of a. Another method of defining a set is by using a rule or semantic description. Use set notation to describe.

These include hat shirt jacket pants and so on. Let s say that our universe contains the numbers 1 2 3 and 4 so u 1 2 3 4. This guide will walk you through the process of making a mathematical venn diagram explaining all the important symbols along the way. Venn diagrams wjec venn diagrams are a useful tool in the world of statistics.

State whether each of the following statements are. A venn diagram consists of multiple overlapping closed curves usually circles each representing a set. This is another example of intensional definition. Other ways of defining sets.